こんにちは!個別指導グノリンクの『小学生の君に送る60秒コラム』を読んでくれてありがとう。
今回のコラムのテーマは『旅人算』です。
『旅人算』は速さの単元の中でも、「流速」や「物体の長さ」が関係してこない文章題ですね。 二人以上の人が向かい合って進む出会い算や、一方が他方を追いかける形で進む追いつき算がメイン です。
速さは苦手!という子も多いですが、どんなところが難しいのかを基本からみていきましょう。
まず攻略したいのは、数字にくっついている「単位」です。
例題:□に当てはまる数を答えましょう
【2.1㎞ を 18分で歩く人の時速は□㎞です】
考え方:速さの主な計算は[速さ][時間][きょり]の3つの要素で行います。
このような考え方を習いましたね。
「きょり÷時間=速さ」
「きょり÷速さ=時間」
「速さ×時間=きょり」
図で教わった人もいるかも知れません。
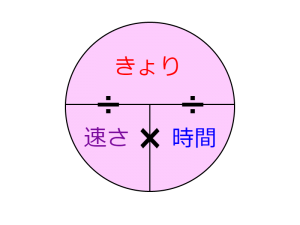
今回の問題に3つの要素を当てはめると、
【2.1㎞ を18分で歩く人の時速は□㎞です】
きょり 時間 速さ
ここまではなんとなくわかるという人も多いですね。
では、
\(\displaystyle\sf2.1㎞\div18分=時速□㎞\) ・・・?
これは違います!
時速□㎞というのは、「1時間で□㎞進む」という意味です。
それに対して、\(\displaystyle\sf2.1㎞\div18分\) で出てくるのは、「1分あたりで進む距離(分速)」なのです。
速さの基本が苦手な人は、まずここで上手く計算が出来ていないことがあります。
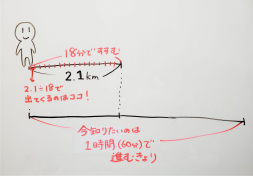
最初に公式だけ丸覚えしてしまうと間違えやすいということももちろんあるのですが、だからといって「イメージして!」と言われてもそれはそれで難しいですよね。
まずは、「今聞かれている□は、2.1kmより多いのかな?少ないのかな?」を考えてみるだけでも間違え にくくなりますよ。
今回聞かれているのは60分で進む距離なので、聞かれている時速は、
\(\displaystyle\sf2.1㎞\div18分\times60=時速7㎞\) \(\sf答え:時速7㎞\)
と出すことが可能です。
または、時速□km=進んだ距離(km)÷進んだ時間(時間) と考えると、
ここがまずあいまいであれば、速さの練習をする前に単位の練習を行いましょう!
(1051字)
今回のコラムのテーマは『旅人算』です。
『旅人算』は速さの単元の中でも、「流速」や「物体の長さ」が関係してこない文章題ですね。 二人以上の人が向かい合って進む出会い算や、一方が他方を追いかける形で進む追いつき算がメイン です。
速さは苦手!という子も多いですが、どんなところが難しいのかを基本からみていきましょう。
まず攻略したいのは、数字にくっついている「単位」です。
例題:□に当てはまる数を答えましょう
【2.1㎞ を 18分で歩く人の時速は□㎞です】
考え方:速さの主な計算は[速さ][時間][きょり]の3つの要素で行います。
このような考え方を習いましたね。
「きょり÷時間=速さ」
「きょり÷速さ=時間」
「速さ×時間=きょり」
図で教わった人もいるかも知れません。

今回の問題に3つの要素を当てはめると、
【2.1㎞ を18分で歩く人の時速は□㎞です】
きょり 時間 速さ
ここまではなんとなくわかるという人も多いですね。
では、
\(\displaystyle\sf2.1㎞\div18分=時速□㎞\) ・・・?
これは違います!
時速□㎞というのは、「1時間で□㎞進む」という意味です。
それに対して、\(\displaystyle\sf2.1㎞\div18分\) で出てくるのは、「1分あたりで進む距離(分速)」なのです。
速さの基本が苦手な人は、まずここで上手く計算が出来ていないことがあります。

最初に公式だけ丸覚えしてしまうと間違えやすいということももちろんあるのですが、だからといって「イメージして!」と言われてもそれはそれで難しいですよね。
まずは、「今聞かれている□は、2.1kmより多いのかな?少ないのかな?」を考えてみるだけでも間違え にくくなりますよ。
今回聞かれているのは60分で進む距離なので、聞かれている時速は、
\(\displaystyle\sf2.1㎞\div18分\times60=時速7㎞\) \(\sf答え:時速7㎞\)
と出すことが可能です。
または、時速□km=進んだ距離(km)÷進んだ時間(時間) と考えると、
\(\displaystyle\sf2.1㎞\div\frac{18}{60}時間=時速7㎞\) \(\sf答え:時速7㎞\)
という式にもできます。(こちらに慣れておくと便利です)ここがまずあいまいであれば、速さの練習をする前に単位の練習を行いましょう!
(1051字)



