こんにちは。個別指導グノリンクの「リンクペディア 3分コラム」を読んでくれてありがとうございます。
本日は東大入試の物理に関するワンポイントアドバイスを述べます。
東大2020年度第一問
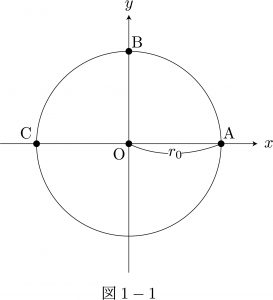
問題: (前問略) (3) 設問I(2)の力$\overrightarrow{F}$を受けながら,小球が図1$-$1の半径$r_0$の円周上を点Aから点Bを通って点Cまで運動したとする。このとき,力$\overrightarrow{F}$が点Aから点Bまでに小球に行う仕事と点Aから点Cまでに小球に行う仕事の大小関係を,理由を含めて答えよ。
この年の力学は大学の学部一年生で扱うような内容絡みの問題でした。そのため,通常高校で教わるような範囲のみの理解でいると,何をしているのかさっぱりだったかもしれません。他方で,学校,塾や予備校で面積速度 (あるいは角運動量) と中心力の関係であったり,積分,ベクトルを用いた仕事の表現を学んでいれば,この大問はつながった一つの大問に見えたことと思います。運動方程式
$$m\frac{d{\overrightarrow{v}}}{dt}=\overrightarrow{F}$$
の両辺のそれぞれの項と$\overrightarrow{v}$との内積をとることで,
$$\frac{d}{dt}\left(\frac{m}{2}|\overrightarrow{v}|^2\right)=\overrightarrow{F}\cdot\overrightarrow{v}$$
という式が得られます。この式は運動エネルギーの時間変化率と仕事率$\overrightarrow{F}\cdot\overrightarrow{v}$の三次元空間における関係です。本問の力$\overrightarrow{F}$が位置ベクトル$\overrightarrow{r}$と平行もしくは反平行であることは,その前の小問で示されています。ただ,これも普段から二次元,三次元のベクトル,ベクトルの成分を用いて力学を勉強していないと,その誘導の意味がわからなかったかもしれません。この前問のヒントに加え,$\overrightarrow{v}$は円軌道の接線方向を向いていることから,$\overrightarrow{F}\cdot\overrightarrow{v}$は各瞬間に0で,円軌道上の運動全体に対してこの仕事率の和をとっても0となります。
もちろん,高校の範囲の知識で答えに行き着けるように東大の問題は工夫されています。ただこの問題に限らず,東大の問題を解く上では高校で教わる内容を「ただ鵜呑みにしているだけ」では,問題がそもそも解けない,あるいは小問の誘導の意味が把握できず時間がかかってしまうということがよくあります。「自分なりに色々調べて」一つ一つの事項を掘り下げる,というのも一つの方法かもしれませんが,果たして高校生が自分で調べるだけで上の方法まで行きつけるのか?というのは疑問です。
また「高校物理では微積分禁止」という噂が特に地方ではよく流れていますが,首都圏の進学校,大手塾,予備校の上位クラスでは上記のようなベクトル,微積分を用いた解説が行われることも珍しくありません。その狙いの一つとして,「物理で用いられる言葉,表現をできるだけ正確に把握する」というものがあるのではないかと筆者は考えています。「比喩などを用いた一見してわかりやすい」説明はもちろんとっつきやすいですが,この方法だと元と異なる意味で言葉を理解してしまうことが少なくありません。東大の問題では過去,その誤解しやすい部分を突いた問題も出題されています。このあたりの情報格差,教育格差の是非についてここで議論したいわけではなく,そのような知識の差が,どういった教え手に出会うかにより生じているという事実を受け止めることにして,それに対して高校生が例えばどういう対策をできるかの候補をここでは述べます。
- 高校物理から少し掘り下げた解説ができる先生のもとで学ぶ (首都圏の高校生はこれがやりやすい。選択肢はかなりある。ただ地方の学生でも,グノリンク含め最近はオンラインでの授業も展開されているのでそういった指導を望むならば授業を受けられる。)
- 市販の参考書 (例:新物理入門 (駿台文庫) ,理論物理への道標 (河合出版) ) を読んで独学
- 独学が厳しい場合,上の参考書を使った勉強をアシストできる先生の補助を受けて勉強する
目先の問題の解説はもちろん色んな先生から受けられますが,その背景の知識まで掘り下げて一貫した物の見方ができる授業を受けられる機会は現実少ないと思われます。どのレベルで「高校物理」を学ぶか,ということについて今一度考えてみると良いかもしれません。