こんにちは!個別指導グノリンクの『小学生の君に送る60秒コラム』を読んでくれてありがとう。
みなさんはガウスの足し算の公式を知っていますか?
公式:(初めの数+最後の数)×個数÷2
算数の授業で習ったことがあるかもしれません。
このガウスというのは人の名前で、正しくはカール・フリードリヒ・ガウスといいます。18世紀から19世紀にたくさんの偉業を残した人です。
ところでこのガウスの足し算ですが、なぜこのような式で計算できるのか説明してみたいと思います。
次の例題と答えを見てください。
みなさんはガウスの足し算の公式を知っていますか?
公式:(初めの数+最後の数)×個数÷2
算数の授業で習ったことがあるかもしれません。
このガウスというのは人の名前で、正しくはカール・フリードリヒ・ガウスといいます。18世紀から19世紀にたくさんの偉業を残した人です。
ところでこのガウスの足し算ですが、なぜこのような式で計算できるのか説明してみたいと思います。
次の例題と答えを見てください。
【例題】
1〜10の連続した整数の和を求めなさい。
【解答】
(1+10)×10÷2=55 答え 55
では解説します。
まず、1~10をそのまま足すのではなく、1〜10をもう1セット用意し下のように1~10を反対にした10~1を並べます。
まず、1~10をそのまま足すのではなく、1〜10をもう1セット用意し下のように1~10を反対にした10~1を並べます。
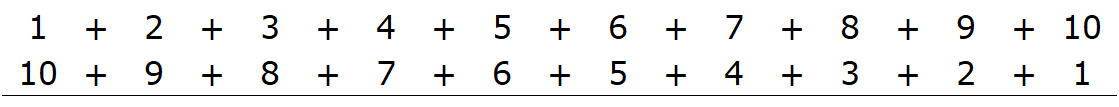
次にそれを縦に足してからすべてを合計します。
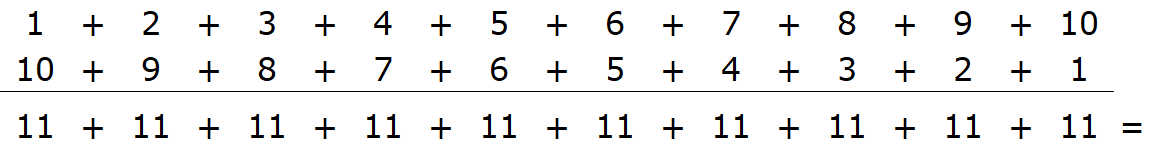
すると、すべて縦の和は11になります。これが10個あるので10倍します。
11×10個=110
ただし、これでは1~10の和と10~1の和の合計で、求めたい1〜10の和の2倍になってしまいますので2で割ります。よって、1~10の和は、
110÷2=55
となります。まとめてすると、
(1+10)×10÷2=55
となり、公式のように計算することができます。
この公式は1からの和だけではなくても使うことができます。
ただし、先ほどの例題のように前後を反対に並べて縦に足したとき数がそろっていないと使えません。また、数は連続していなくても使えます。つまり、差が等しい数の並び(等差数列)の和ならばこの公式が使えます。(2+5+8+11……+32のような)
ちなみに、この公式はガウスが7歳のときに学校の先生から1から100を全部足してみなさいと言われて考え出したという話が残っています。
また、言葉を話し出す前にすでに計算感覚があったようで、レンガ会社の社長をしていた父親が自分の会社の給料の計算をしていたとき、そばで見ていたガウスがまちがいを指摘し、父親が計算し直したら確かに計算をまちがえていたようです。このときガウスは3歳だったそうです。
本当かどうかわかりませんが、ガウスにはこういう逸話がたくさん残っています。こういう人を天才というのでしょうね。
(1061字)
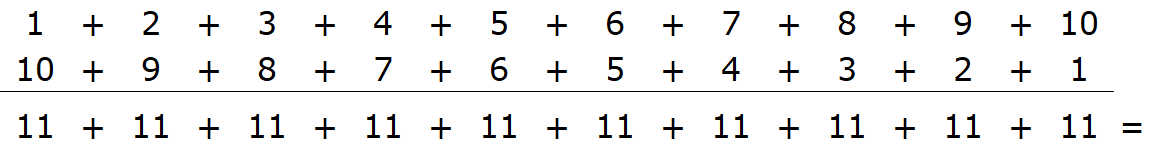
すると、すべて縦の和は11になります。これが10個あるので10倍します。
11×10個=110
ただし、これでは1~10の和と10~1の和の合計で、求めたい1〜10の和の2倍になってしまいますので2で割ります。よって、1~10の和は、
110÷2=55
となります。まとめてすると、
(1+10)×10÷2=55
となり、公式のように計算することができます。
この公式は1からの和だけではなくても使うことができます。
ただし、先ほどの例題のように前後を反対に並べて縦に足したとき数がそろっていないと使えません。また、数は連続していなくても使えます。つまり、差が等しい数の並び(等差数列)の和ならばこの公式が使えます。(2+5+8+11……+32のような)
ちなみに、この公式はガウスが7歳のときに学校の先生から1から100を全部足してみなさいと言われて考え出したという話が残っています。
また、言葉を話し出す前にすでに計算感覚があったようで、レンガ会社の社長をしていた父親が自分の会社の給料の計算をしていたとき、そばで見ていたガウスがまちがいを指摘し、父親が計算し直したら確かに計算をまちがえていたようです。このときガウスは3歳だったそうです。
本当かどうかわかりませんが、ガウスにはこういう逸話がたくさん残っています。こういう人を天才というのでしょうね。
(1061字)



