こんにちは!個別指導グノリンクの『小学生の君に送る60秒コラム』を読んでくれてありがとう。
今回のコラムは『旅人算』の応用で、「ダイヤグラム」を使った問題について考えてみましょう。
ダイヤグラムとは、この場合速さのグラフを表します。
旅人算の中で、特にダイヤグラムを使った方が便利な問題は、「何往復もする」タイプの問題です。例題を見てみましょう。
今回のコラムは『旅人算』の応用で、「ダイヤグラム」を使った問題について考えてみましょう。
ダイヤグラムとは、この場合速さのグラフを表します。
旅人算の中で、特にダイヤグラムを使った方が便利な問題は、「何往復もする」タイプの問題です。例題を見てみましょう。
【例題】
直線上に2つの点A、Bがあり、点Pと点Qが同時に点Aを出発してAB間を往復します。
ただし、点A、点Bに到着するごとに、点Pは8秒間、点Qは4秒間休みます。
ABの長さが112cm、点P、点Qの速さがそれぞれ秒速8cm、秒速4cmとします。
点P、点Qが2度目に出会うのは点Aから何cmのところですか。
文章内の数字が多く、「往復する」「休む」「二度目に出会う」などの条件があるためややこしくなっていますね。
では、これをダイヤグラムで解くとどうなるのか見てみましょう。
では、これをダイヤグラムで解くとどうなるのか見てみましょう。
考え方
ダイヤグラムに点P(青い線)と点Q(オレンジの線)のうごきをまとめてみます。
点Pは秒速8cmなので 112÷8=14 より、Bに行くまで14秒、
点Qは秒速4cmなので 112÷4=28 より、Bに行くまで28秒かかります。
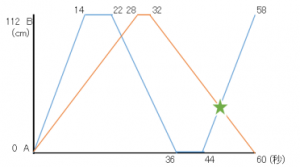
このような形にまとめられます。
今出したい点P、点Qが2度目に出会う地点は★マークのところです。
ダイヤグラムの便利なところは「図形のように相似や比が使える」点です。
今回は相似を使って解いてみましょう。
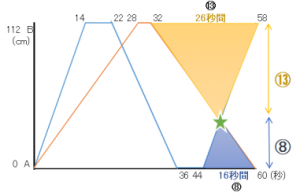
★マークの上下に三角形を作ると、砂時計型の相似になっていることがわかります。 上の△は底辺が26、下の△は底辺が16になるので、相似比は26:16=13:8です。
相似比は高さの比にも使うことが出来ます。上の△の高さを⑬、下の△の高さを⑧とおいてみましょう。
ダイヤグラムは、上手く使えるようになるとぐっと便利になります。
是非練習してみてくださいね。
(1043字)
点Pは秒速8cmなので 112÷8=14 より、Bに行くまで14秒、
点Qは秒速4cmなので 112÷4=28 より、Bに行くまで28秒かかります。

このような形にまとめられます。
今出したい点P、点Qが2度目に出会う地点は★マークのところです。
ダイヤグラムの便利なところは「図形のように相似や比が使える」点です。
今回は相似を使って解いてみましょう。

★マークの上下に三角形を作ると、砂時計型の相似になっていることがわかります。 上の△は底辺が26、下の△は底辺が16になるので、相似比は26:16=13:8です。
相似比は高さの比にも使うことが出来ます。上の△の高さを⑬、下の△の高さを⑧とおいてみましょう。
\(\displaystyle\sf⑬+⑧=112㎝\) ⇒ \(\displaystyle\sf㉑=112㎝\) なので、\(\displaystyle\sf①=5\frac{1}{3}㎝\)です。
「点Aから何cm」をきかれているので、⑧を出しましょう。\(\displaystyle\sf⑧=5\frac{1}{3\times8=42\frac{2}{3}\) \(\displaystyle\sf答え:42\frac{2}{3}㎝\)
いかがでしたでしょうか。ダイヤグラムは、上手く使えるようになるとぐっと便利になります。
是非練習してみてくださいね。
(1043字)



