こんにちは！個別指導グノリンクの『小学生の君に送る６０秒コラム』を読んでくれてありがとう。

算数の特殊算のポイントシリーズ、今回のテーマは【つるかめ算～基本編～】です。

「つるかめ算はわかるのだけれど、面積図にしようとするとよくわからなくなってしまう」

「文章題を読んでもつるかめ算だということになかなか気が付けない」

そんな人にぜひ読んでもらいたいです！

つるかめ算というと次のような問題が基本です。

問１「ひと箱7枚入りのクッキーとひと箱４枚入りのクッキーを合わせて１０箱買ったらクッキーの数は５８枚になりました。７枚入りの箱は何箱買いましたか？」

こちらの問題の面積図はかけるでしょうか？

今回はクッキーという数えやすいものの問題なので、イメージをしながら取り組んでみて下さい。

(左側がイメージ、右側が実際の図です)

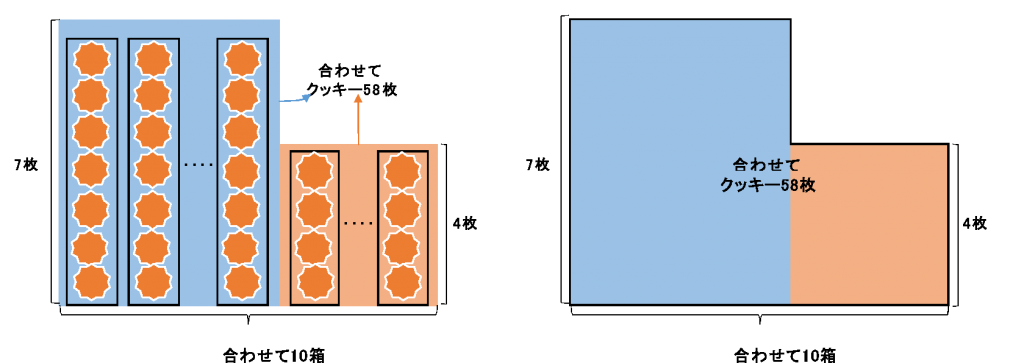
【1箱に入っているクッキーの枚数】×【箱の数】＝【クッキーの合計枚数】

というかけ算なので、かけ算の答えである【クッキーの合計枚数】が面積になります。

「７枚入りの箱は何箱」という質問なので、知りたいのは水色のところの横はばです。

…さて、では上の面積図からどのような式が作れるかを考えてみましょう！ 大きく分けて２パターン考えることが出来ます。

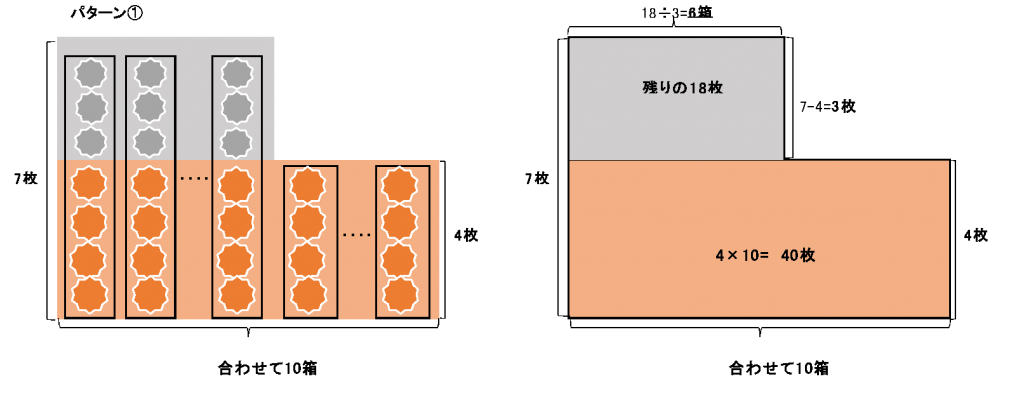
パターン①：4×10=40…下のピンクの段　

58－40＝18…グレーの部分　

18÷(7－4)＝６(箱)

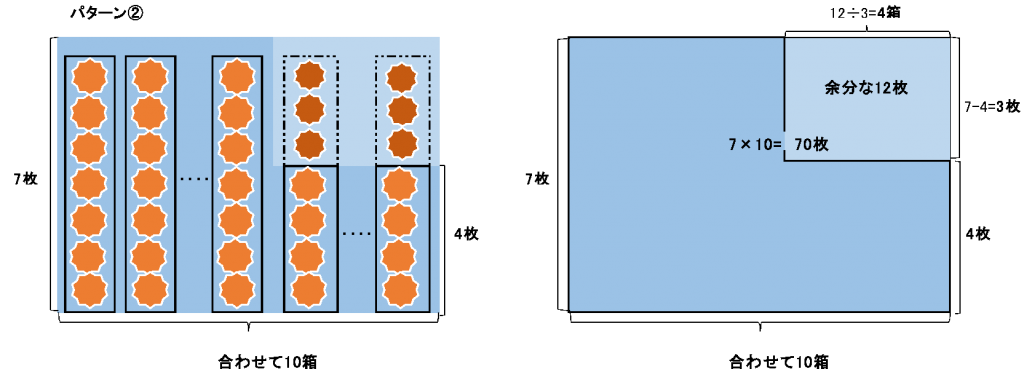
パターン②：7×10＝70(水色全部)

　70－58＝12(うすい水色のところ)

12÷(7－4)＝4(これは4枚の箱数になります)

10－4＝6(箱)

「こんなの簡単だよ！」という上級生も多いかもしれませんね。

では、パターン①とパターン②に共通している考え方はなんだかわかるでしょうか？

それは、

両方とも「もしも１０箱全部が《4枚入りまたは7枚入り》だったら？」という考え方を使っているということです。

「もし全部が〇〇だったら？」

これが、つるかめ算にとりくむ・気付く上で大切なポイントとなります！覚えておいてくださいね。

次回算数、【つるかめ算～応用編～】に続きます。

(863文字)

投稿タグ
, , , ,