こんにちは!個別指導グノリンクの『小学生の君に送る60秒コラム』を読んでくれてありがとう。
今回のコラムは、「対角線の本数」について考えてみます。
問:正五角形の対角線の数は何本でしょう
この問題でいう対角線とは、隣り合わない二つの頂点を結ぶ線分のことです。
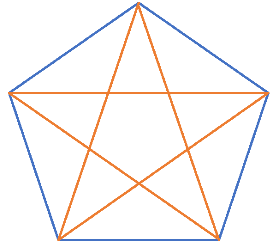
下の図でいうと、黄色の線が対角線ですね。
数えてみると星形に5本引けることが分かりますので、問の答えは5本です。
ですが、もしこの問題が正十角形だったら…図に描くのは難しいですよね。
そこで、対角線の本数を出す式について考えてみましょう。
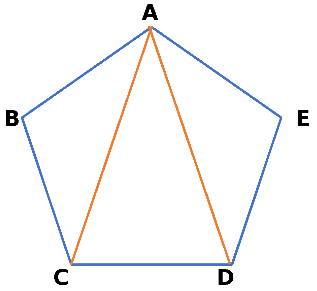
この五角形の5つの頂点を A,B,C,D,E とします。
Aからひくことのできる対角線は、CへとDへの2本です。
AとB、AとEはそれぞれ隣り合っており、辺がつながっているため対角線はひけません。
5つ頂点があるうち、自分自身(A)と両隣(B、E)には対角線がひけないので、これは5-3=2(本)と表すことができます。
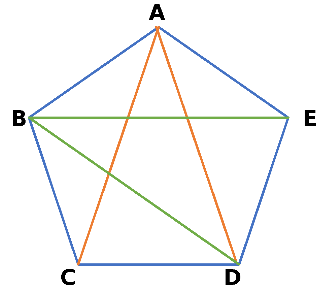
同じようにBからもDへとEへの2本の対角線をひくことができます。
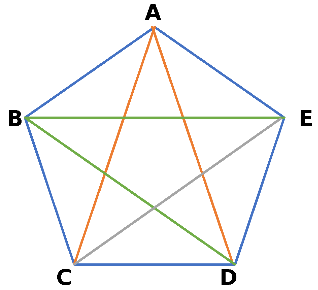
次にCからひこうとすると…Aにはすでに黄色の線があるので、Eへの1本だけになりますね。
D、Eからももうすでに線がひいてあるのでこれ以上の線はひけません。
ここまでをまとめると、
①正五角形の一つの頂点からひける線は2本 (5−3=2)
②もうすでに線がひいてあるところには、重ねて線をひくことができない
ということがわかりました。
では、このことから対角線の本数を出す式を作ってみましょう。
正五角形の一つの頂点からひける対角線は5−3=2(本)、頂点は全部で5つありますので、これだけですと対角線は(5−3)×5ひけることになります。
ですがこのままだと、「AからC」と「CからA」のように同じところに線を2本ずつひいていることになってしまいますので、重ならないように÷2が必要です。
よって正五角形の対角線の本数は
(5−3)×5÷2=5(本)
と式で求めることができます。
これがもし正十角形であれば、①の一つの頂点からひける線の本数は 10−3=7(本) になります。
頂点が全部で10個、重ならないよう÷2をすると、
(10−3)×10÷2=35で、正十角形の対角線の本数は35本ということがわかります。
このように、正n角形の対角線の本数は(n−3)×n÷2で出すことができるのです。
ぜひ覚えておいてくださいね。
(963文字)
- 投稿タグ
- 中学受験 塾 勉強 家庭学習



